Given a binary tree root, a ZigZag path for a binary tree is defined as follow:
- Choose any node in the binary tree and a direction (right or left).
- If the current direction is right then move to the right child of the current node otherwise move to the left child.
- Change the direction from right to left or right to left.
- Repeat the second and third step until you can't move in the tree.
Zigzag length is defined as the number of nodes visited - 1. (A single node has a length of 0).
Return the longest ZigZag path contained in that tree.
Example 1:
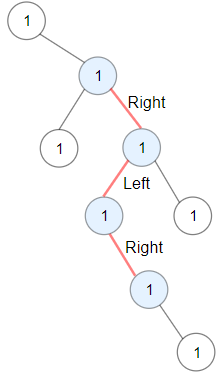
Input: root = [1,null,1,1,1,null,null,1,1,null,1,null,null,null,1,null,1] Output: 3 Explanation: Longest ZigZag path in blue nodes (right -> left -> right).
Example 2:
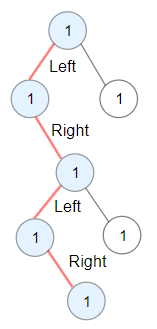
Input: root = [1,1,1,null,1,null,null,1,1,null,1] Output: 4 Explanation: Longest ZigZag path in blue nodes (left -> right -> left -> right).
Example 3:
Input: root = [1] Output: 0
Constraints:
- Each tree has at most
50000nodes.. - Each node's value is between
[1, 100].
Answer:
For question involving tree, recursion around its root/left/right child is always good starting point.
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { /* * Recursive return [left, right, result], where: * left is the maximum length in direction of root.left * right is the maximum length in direction of root.right * result is the maximum length in the whole sub tree. * * Complexity * Time O(N) * Space O(height) */ // my old answer, not right. // Integer result = 0; // public int longestZigZag(TreeNode root) { // checkLongestZigZag(root, false); // checkLongestZigZag(root, true); // return result; // } // private int checkLongestZigZag(TreeNode node, boolean isLeft) { // if (node == null) { // return -1; // } // TreeNode next = isLeft? node.right : node.left; // TreeNode theOther = isLeft? node.left : node.right; // int nextResult = checkLongestZigZag(next, !isLeft); // int theOtherResult = checkLongestZigZag(theOther, isLeft); // result = Math.max(Math.max(nextResult + 1, theOtherResult), result); // return (nextResult + 1); // } public int longestZigZag(TreeNode root) { return dfs(root)[2]; } private int[] dfs(TreeNode root) { if (root == null) return new int[]{-1, -1, -1}; int[] left = dfs(root.left), right = dfs(root.right); int res = Math.max(Math.max(left[1], right[0]) + 1, Math.max(left[2], right[2])); return new int[]{left[1] + 1, right[0] + 1, res}; } }
No comments:
Post a Comment