124 Binary Tree Maximum Path Sum

Hello, guys. It has been such a long time since this blog was updated. Solving problems is an endless adventure. I am really happy that I am still in the trip.

Back to our topic, let's take a look at this problem in leetcode.

Given a non-empty binary tree, find the maximum path sum.

For this problem, a path is defined as any node sequence from some starting node to any node in the tree along the parent-child connections. The path must contain at least one node and does not need to go through the root.

 

Example 1:

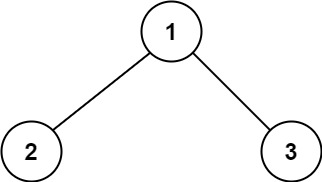
Input: root = [1,2,3]
Output: 6

Example 2:

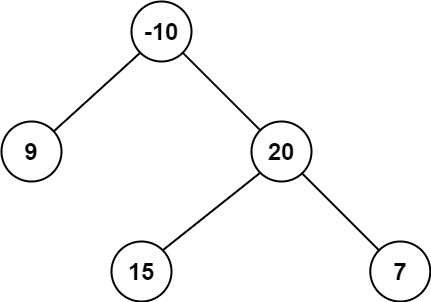
Input: root = [-10,9,20,null,null,15,7]
Output: 42

 

Constraints:

• The number of nodes in the tree is in the range [0, 3 * 104].
• -1000 <= Node.val <= 1000

Dealing with problems of tree usually needs recursion as a hand. This is due to the special structure of tree. The structure of tree is also a recursion.

Thanks to code ganker's helpful tips.  One key point of this question is that if max sum of one root can be max sum of left subtree, plus value of root, plus max sum of right subtree, however, when one node is needed to connect to its parent, only its left or right subtree, plus its own value should be used.  Another good point I didn't think of is that if left or right subtree return negative value, root would add nothing than adding negatives.

Below is the code:

 public class Solution {  
   public int maxPathSum(TreeNode root) {  
     if (root == null) return 0;  
     ArrayList<Integer> res = new ArrayList<Integer>();  
     res.add(Integer.MIN_VALUE);  
     helper(root,res);  
     return res.get(0);  
   }  
   public int helper(TreeNode root, ArrayList<Integer> res){  
     if (root == null) return 0;  
     int left = helper(root.left, res);  
     int right = helper(root.right, res);  
     int result = root.val + (left>0?left:0) + (right>0?right:0);  
     if (result > res.get(0)){  
       res.set(0, result);  
     }  
     return root.val + Math.max(left, Math.max(right,0));  
   }  
 }  

UPDATED: my answer in late 2020

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    int maxSum = Integer.MIN_VALUE;
    public int maxPathSum(TreeNode root) {
        helper(root);
        return maxSum;
    }
    
    private int[] helper(TreeNode node) {
        int[] result = new int[2];
        if (node == null) {
            return result;
        }
        int[] leftResult = helper(node.left);
        int[] rightResult = helper(node.right);
        // sum value can be connected to parent
        // note: parent can choose to ignore negative values
        result[0] = node.val + Math.max(0, Math.max(leftResult[0], rightResult[0]));
        // sum value disconnected to parent
        result[1] = node.val + Math.max(0, leftResult[0]) + Math.max(0, rightResult[0]);
        
        maxSum = Math.max(maxSum, result[1]);
        return result;
    }
}