Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
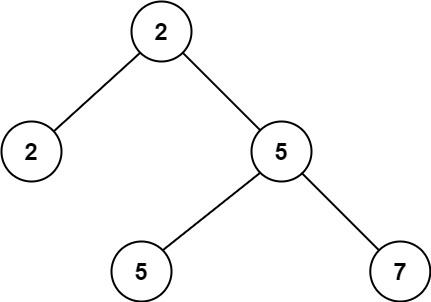
Example 1:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 Output: 3 Explanation: The LCA of nodes 5 and 1 is 3.
Example 2:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 Output: 5 Explanation: The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.
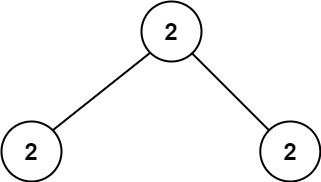
Example 3:
Input: root = [1,2], p = 1, q = 2 Output: 1
Constraints:
- The number of nodes in the tree is in the range
[2, 105]. -109 <= Node.val <= 109- All
Node.valare unique. p != qpandqwill exist in the tree.
This is similar to question 235:
My answer: recursive
Other solutions: non-recursion: use hash map to store node -> parent, and find all parents of p, q and find the lowest common one.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | /** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */ class Solution { public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) { if (root == null || root == p || root == q) { return root; } TreeNode leftResult = lowestCommonAncestor(root.left, p, q); TreeNode rightResult = lowestCommonAncestor(root.right, p, q); if (leftResult == null && rightResult == null) { return null; } else if (leftResult == null) { return rightResult; } else if (rightResult == null) { return leftResult; } else { return root; } } } |